Big O

Notation

😲

O

What's the idea here?

Imagine we have multiple implementations of the same function.

How can we determine which one is the "best?"

Imagine we have multiple implementations of the same function.

How can we determine which one is the "best?"

"Write a function that accepts a string input and returns a reversed copy"

Great!

Pretty Good

Only OK

Ehhhhh

Awful

Who Cares?

It's important to have a precise vocabulary to talk about how our code performs
Useful for discussing trade-offs between different approaches
When your code slows down or crashes, identifying parts of the code that are inefficient can help us find pain points in our applications
Also important: it comes up in interviews! (but imo it's a terrible topic to ask about in an interview)

Who Cares?

It's important to have a precise vocabulary to talk about how our code performs
Useful for discussing trade-offs between different approaches
When your code slows down or crashes, identifying parts of the code that are inefficient can help us find pain points in our applications
Also important: it comes up in interviews! (but imo it's a terrible topic to ask about in an interview)

An Example

function addUpTo(n) {
  let total = 0;
  for (let i = 1; i <= n; i++) {
    total += i;
  }
  return total;
}

Suppose we want to write a function that calculates the sum of all numbers from 1 up to (and including) some number n.

function addUpTo(n) {
  return n * (n + 1) / 2;
}

Which one is better?

An Example

Which one is better?

What does better mean?

Faster?
Less memory-intensive?
More readable?

Let's focus here first

Faster?
Less memory-intensive?
More readable?

Why not use timers?

function addUpTo(n) {
  let total = 0;
  for (let i = 1; i <= n; i++) {
    total += i;
  }
  return total;
}

let t1 = performance.now();
addUpTo(1000000000);
let t2 = performance.now();
console.log(`Time Elapsed: ${(t2 - t1) / 1000} seconds.`)

Why not use timers?

The Problem with Time

Different machines will record different times
The same machine will record different times!
For fast algorithms, speed measurements may not be precise enough?

If not time, then what?

Rather than counting seconds, which are so variable...

Let's count the number of simple operations the computer has to perform!

Counting Operations

function addUpTo(n) {
  return n * (n + 1) / 2;
}

1 multiplication

1 addition

1 division

3 simple operations, regardless of the size of n

Counting Operations

function addUpTo(n) {
  let total = 0;
  for (let i = 1; i <= n; i++) {
    total += i;
  }
  return total;
}

n additions

n assignments

n additions and n assignments

1 assignment

n comparisons

?????

Counting is hard!

Depending on what we count, the number of operations can be as low as 2n or as high as 5n + 2

But regardless of the exact number, the number of operations grows roughly proportionally with n

If n doubles, the number of operations will also roughly double

Introducing....Big O

Big O Notation is a way to formalize fuzzy counting

It allows us to talk formally about how the runtime of an algorithm grows as the inputs grow

We won't care about the details, only the trends

Big O Definition

We say that an algorithm is O(f(n)) if the number of simple operations the computer has to do is eventually less than a constant times f(n), as n increases

f(n) could be linear (f(n) = n)
f(n) could be quadratic (f(n) = n )
f(n) could be constant (f(n) = 1)
f(n) could be something entirely different!

Example

function addUpTo(n) {
  return n * (n + 1) / 2;
}

function addUpTo(n) {
  let total = 0;
  for (let i = 1; i <= n; i++) {
    total += i;
  }
  return total;
}

Always 3 operations

O(1)

Number of operations is (eventually) bounded by a multiple of n (say, 10n)

O(n)

Another Example

function countUpAndDown(n) {
  console.log("Going up!");
  for (let i = 0; i < n; i++) {
    console.log(i);
  }
  console.log("At the top!\nGoing down...");
  for (let j = n - 1; j >= 0; j--) {
    console.log(j);
  }
  console.log("Back down. Bye!");
}

Number of operations is (eventually) bounded by a multiple of n (say, 10n)

O(n)

YET ANOTHER EXAMPLE

function printAllPairs(n) {
  for (var i = 0; i < n; i++) {
    for (var j = 0; j < n; j++) {
      console.log(i, j);
    }
  }
}

O(n) operation inside of an O(n) operation.

O(n * n)

O(n)

O(n )

Simplifying Big O Expressions

When determining the time complexity of an algorithm, there are some helpful rule of thumbs for big O expressions.

These rules of thumb are consequences of the definition of big O notation.

Constants Don't Matter

O(2n)

O(500)

O(13n )

O(n)

O(1)

O(n )

Smaller Terms Don't Matter

O(n + 10)

O(1000n + 50)

O(n + 5n + 8 )

O(n)

O(n )

Big O Shorthands

Analyzing complexity with big O can get complicated
There are several rules of thumb that can help
These rules won't ALWAYS work, but are a helpful starting point

Big O Shorthands

Arithmetic operations are constant
Variable assignment is constant
Accessing elements in an array (by index) or object (by key) is constant
In a loop, the the complexity is the length of the loop times the complexity of whatever happens inside of the loop

A Couple More Examples

function logAtLeast5(n) {
  for (var i = 1; i <= Math.max(5, n); i++) {
    console.log(i);
  }
}

function logAtMost5(n) {
  for (var i = 1; i <= Math.min(5, n); i++) {
    console.log(i);
  }
}

O(n)

O(1)

O(1)

O(log n)

O(n)

O(nlog n)

O(n )

Space Complexity

So far, we've been focusing on time complexity: how can we analyze the runtime of an algorithm as the size of the inputs increases?

We can also use big O notation to analyze space complexity: how much additional memory do we need to allocate in order to run the code in our algorithm?

What about the inputs?

Sometimes you'll hear the term auxiliary space complexity to refer to space required by the algorithm, not including space taken up by the inputs.

Unless otherwise noted, when we talk about space complexity, technically we'll be talking about auxiliary space complexity.

Space Complexity in JS

Rules of Thumb

Most primitives (booleans, numbers, undefined, null) are constant space
Strings require O(n) space (where n is the string length)
Reference types are generally O( n), where n is the length (for arrays) or the number of keys (for objects)

An Example

function sum(arr) {
  let total = 0;
  for (let i = 0; i < arr.length; i++) {
    total += arr[i];
  }
  return total;
}

one number

another number

O(1) space!

Another Example

function double(arr) {
  let newArr = [];
  for (let i = 0; i < arr.length; i++) {
    newArr.push(2 * arr[i]);
  }
  return newArr;
}

n numbers

O(n) space!

YOUR

TURN

Logarithms

We've encountered some of the most common complexities: O(1), O(n), O(n )

Sometimes big O expressions involve more complex mathematical expressions

One that appears more often than you might like is the logarithm!

Wait, what's a log again?

log (8) = 3

2 = 8

log (value) = exponent

2 = value

exponent

We'll omit the 2.

log === log

Wut.

This isn't a math course, so here's a rule of thumb.

The logarithm of a number roughly measures the number of times you can divide that number by 2 before you get a value that's less than or equal to one.

Logarithm Examples

12.5

6.25

3.125

1.5625

0.78125

log(8) = 3

log(25) ≈ 4.64

÷ 2

Logarithm Complexity

Logarithmic time complexity is great!

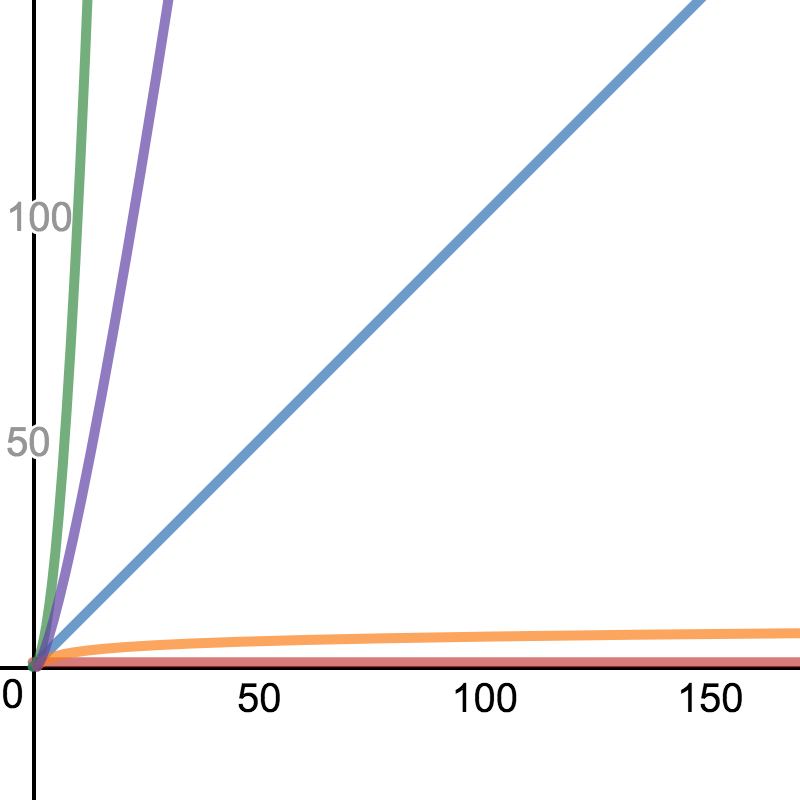
O(1)

O(log n)

O(n)

O(nlog n)

O(n )

Who Cares?

Certain searching algorithms have logarithmic time complexity.

Efficient sorting algorithms involve logarithms.

Recursion sometimes involves logarithmic space complexity.

...and more!

Recap

To analyze the performance of an algorithm, we use Big O Notation
Big O Notation can give us a high level understanding of the time or space complexity of an algorithm
Big O Notation doesn't care about precision, only about general trends (linear? quadratic? constant?)
The time or space complexity (as measured by Big O) depends only on the algorithm, not the hardware used to run the algorithm
Big O Notation is everywhere, so get lots of practice!