DYNAMIC PROGRAMMING
A Light Introduction
A Light Introduction
DON'T BE SCARED
(I am)
RECURSION
Make sure you're Ok With
OBJECTIVES
- Define what dynamic programming is
- Explain what overlapping subproblems are
- Understand what optimal substructure is
- Solve more challenging problems using dynamic programming
- Define what dynamic programming is
- Explain what overlapping subproblems are
- Understand what optimal substructure is
- Solve more challenging problems using dynamic programming
OBJECTIVES
WTF IS
DYNAMIC PROGRAMMING
"A method for solving a complex problem by breaking it down into a collection of simpler subproblems, solving each of those subproblems just once, and storing their solutions."
Where does
the name come from?
IT ONLY WORKS ON PROBLEMS WITH...
Optimal Substructure &
Overlapping Subproblems
EXCUSE ME?!
EXCUSE ME?!
OVERLAPPING
SUBPROBLEMS
A problem is said to have overlapping subproblems if it can be broken down into subproblems which are reused several times
"Every number after the first two is the sum of the two preceding ones"
FIBONACCI SEQUENCE
FIBONACCI SEQUENCE
1
1
2
3
5
8
13
1
1
2
3
5
8
13
fib(5)
fib(5)
fib(5)
fib(4)
fib(5)
fib(3)
fib(5)
fib(3)
fib(5)
fib(2)
fib(5)
fib(2)
fib(5)
fib(1)
fib(5)
fib(2)
fib(5)
fib(1)
+
+
+
+
FIBONNACI NUMBERS
WE'RE REPEATING THINGS!
OVERLAPPING SUBPROBLEMS!
OVERLAPPING SUBPROBLEMS!
mergeSort([10,24,76,73])
mergeSort([10,24])
mergeSort([76,73])
mergeSort([76])
mergeSort([73])
mergeSort([10])
mergeSort([24])
[10]
[24]
[10,24]
[73,76]
[76]
[73]
merge
merge
merge
[10,24,73,76]
REMEMBER MERGESORT?
REMEMBER MERGESORT?
NO OVERLAPPING SUBPROBLEMS!
NO OVERLAPPING SUBPROBLEMS!
mergeSort([10,24,10,24])
mergeSort([10,24])
mergeSort([10,24])
mergeSort([10])
mergeSort([24])
mergeSort([10])
mergeSort([24])
A VERY SPECIAL CASE
REMEMBER MERGESORT?
YES OVERLAPPING SUBPROBLEMS!
NO OVERLAPPING SUBPROBLEMS!
OPTIMAL SUBSTRUCTURE
A problem is said to have optimal substructure if an optimal solution can be constructed from optimal solutions of its subproblems
A
B
E
D
SHORTEST PATH FROM:
A to D
A to C
A to B
A -> B -> C -> D
SHORTEST PATH
C
2
2
2
3
1
A -> B -> C
A -> B
OPTIMAL SUBSTRUCTURE!
A
B
C
D
LONGEST PATH FROM:
A to C
C to D
A to D
A -> B -> C
C -> B -> D
LONGEST SIMPLE PATH
(simple means no repeating)
A -> B -> C -> B -> D
A -> B -> D
NO OPTIMAL SUBSTRUCTURE!
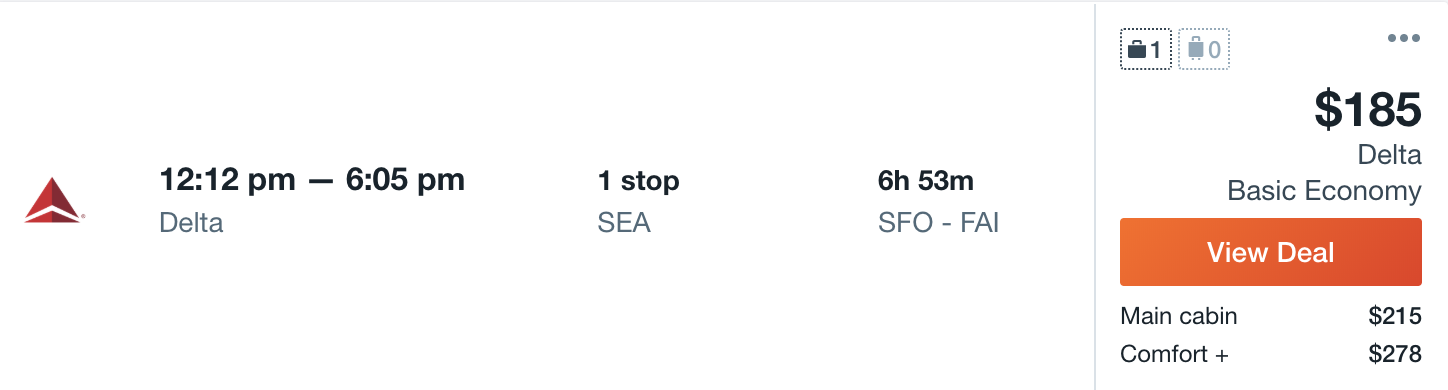

Cheapest flight from SFO to FAI?
SFO
SEA
FAI
Cheapest flight from SFO to SEA?
PDX
SFO
SEA
NO OPTIMAL SUBSTRUCTURE!


Cheapest flight from SFO to FAI?
SFO
SEA
FAI
Cheapest flight from SFO to SEA?
PDX
SFO
SEA
NO OPTIMAL SUBSTRUCTURE!
THE FIBONACCI SEQUENCE
Let's return to our pal...
THE FIBONACCI SEQUENCE
LET'S WRITE IT!
A MEMO-IZED SOLUTION
- Fib(n) = Fib(n-1) + Fib(n-2)
- Fib(2) is 1
- Fib(1) is 1
function fib(n){
if(n <= 2) return 1;
return fib(n-1) + fib(n-2);
}RECURSIVE SOLUTION
A MEMO-IZED SOLUTION
fib(5)
fib(5)
fib(5)
fib(4)
fib(5)
fib(3)
fib(5)
fib(3)
fib(5)
fib(2)
fib(5)
fib(2)
fib(5)
fib(1)
fib(5)
fib(2)
fib(5)
fib(1)
+
+
+
+
PLAIN OLD RECURSION
1
1
2
2
1
1
1
3
5
Big O
LET'S CHAT ABOUT
Big O
LET'S CHAT ABOUT
fib(5)
fib(5)
fib(5)
fib(4)
fib(5)
fib(3)
fib(5)
fib(3)
fib(5)
fib(2)
fib(5)
fib(1)
fib(5)
fib(1)
fib(5)
fib(2)
fib(5)
fib(1)
+
+
+
+
fib(6)
fib(6)
fib(5)
fib(6)
fib(4)
fib(6)
fib(4)
fib(6)
fib(3)
fib(6)
fib(3)
fib(6)
fib(2)
fib(6)
fib(3)
fib(6)
fib(2)
fib(6)
fib(2)
fib(6)
fib(1)
fib(6)
fib(1)
fib(6)
fib(2)
fib(6)
fib(1)
fib(6)
fib(2)
fib(6)
fib(7)
fib(6)
fib(5)
fib(5)
fib(4)
fib(4)
fib(4)
fib(3)
fib(3)
fib(3)
fib(3)
fib(2)
fib(2)
fib(2)
fib(2)
fib(2)
fib(2)
fib(2)
fib(2)
fib(3)
fib(1)
fib(1)
fib(1)
fib(1)
fib(1)
https://i.stack.imgur.com/kgXDS.png
Look at that growth!
Look at that growth!
HOW BAD?
O(2 )
n
HOW BAD?
HOW BAD?
O(2 )
n
HOW BAD?
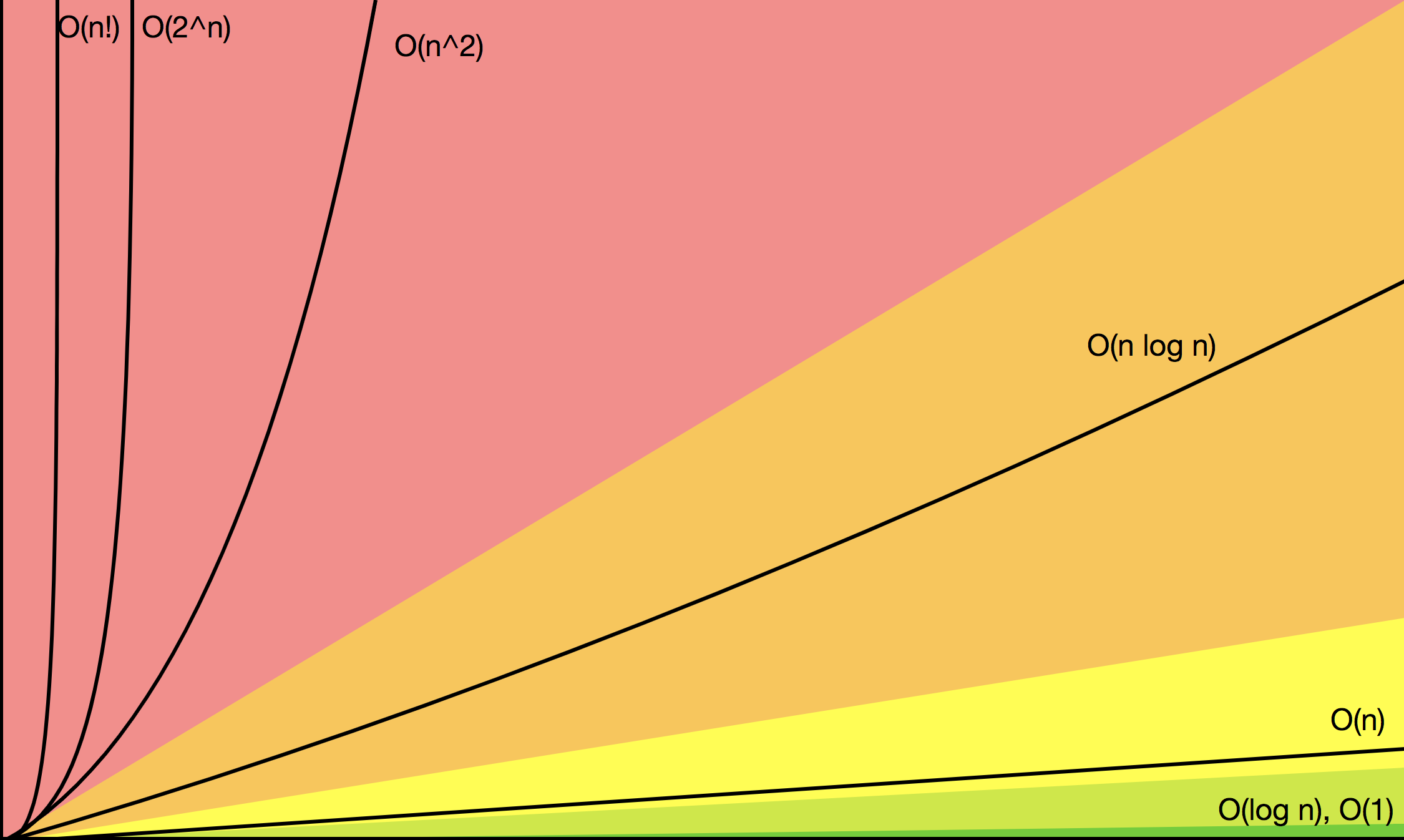
https://i.stack.imgur.com/kgXDS.png
THAT BAD
WHAT CAN WE IMPROVE??
WHAT CAN WE IMPROVE??
fib(5)
fib(5)
fib(5)
fib(4)
fib(5)
fib(3)
fib(5)
fib(3)
fib(5)
fib(2)
fib(5)
fib(1)
fib(5)
fib(1)
fib(5)
fib(2)
fib(5)
fib(1)
+
+
+
+
WE'RE REPEATING THINGS!
WE'RE REPEATING THINGS!
fib(6)
fib(6)
fib(5)
fib(6)
fib(4)
fib(6)
fib(4)
fib(6)
fib(3)
fib(6)
fib(3)
fib(6)
fib(2)
fib(6)
fib(3)
fib(6)
fib(2)
fib(6)
fib(2)
fib(6)
fib(1)
fib(6)
fib(1)
fib(6)
fib(2)
fib(6)
fib(1)
fib(6)
fib(2)
fib(6)
THIS IS NOT GOOD.
WE'RE REPEATING THINGS!
fib(7)
fib(6)
fib(5)
fib(5)
fib(4)
fib(4)
fib(4)
fib(3)
fib(3)
fib(3)
fib(3)
fib(2)
fib(2)
fib(2)
fib(2)
fib(2)
fib(2)
fib(2)
fib(2)
fib(3)
fib(1)
fib(1)
fib(1)
fib(1)
fib(1)
REALLY NOT GOOD
WE'RE REPEATING THINGS!
WHAT IF WE COULD
"REMEMBER" OLD VALUES?
WHAT IF WE COULD
"REMEMBER" OLD VALUES?
ENTER
DYNAMIC PROGRAMMING
"Using past knowledge to make solving a future problem easier"
ENTER (AGAIN)
DYNAMIC PROGRAMMING
"A method for solving a complex problem by breaking it down into a collection of simpler subproblems, solving each of those subproblems just once, and storing their solutions."
MEMOIZATION
Storing the results of expensive function calls and returning the cached result when the same inputs occur again
MEMOIZATION
Storing the results of expensive function calls and returning the cached result when the same inputs occur again
function fib(n, memo=[]){
if(memo[n] !== undefined) return memo[n]
if(n <= 2) return 1;
var res = fib(n-1, memo) + fib(n-2, memo);
memo[n] = res;
return res;
}A MEMO-IZED SOLUTION
A MEMO-IZED SOLUTION
fib(5)
fib(5)
fib(5)
fib(4)
fib(5)
fib(3)
fib(5)
fib(3)
fib(5)
fib(2)
fib(5)
fib(2)
fib(5)
fib(1)
fib(5)
fib(2)
fib(5)
fib(1)
+
+
+
+
1
1
2
2
1
3
5
0
1
2
3
4
5
1
1
2
3
5
X
What we've already calculated
RECURSION + MEMOIZATION
Big O
LET'S CHAT ABOUT
Big O
LET'S CHAT ABOUT
fib(7)
fib(6)
fib(5)
fib(5)
fib(4)
fib(4)
fib(4)
fib(3)
fib(3)
fib(3)
fib(3)
fib(2)
fib(2)
fib(2)
fib(2)
fib(2)
fib(2)
fib(2)
fib(2)
fib(3)
fib(1)
fib(1)
fib(1)
fib(1)
fib(1)
MUCH BETTER
O(n)
MUCH BETTER

Once Again
DYNAMIC PROGRAMMING
"A method for solving a complex problem by breaking it down into a collection of simpler subproblems, solving each of those subproblems just once, and storing their solutions."
WE'VE BEEN WORKING
TOP-DOWN
BUT THERE IS ANOTHER WAY!
BOTTOM-UP
Tabulation
Storing the result of a previous result in a "table" (usually an array)
Usually done using iteration
Better space complexity can be achieved using tabulation
Tabulation
function fib(n){
if(n <= 2) return 1;
var fibNums = [0,1,1];
for(var i = 3; i <= n; i++){
fibNums[i] = fibNums[i-1] + fibNums[i-2];
}
return fibNums[n];
}TABULATED VERSION
TABULATED VERSION
0
1
2
3
4
5
1
1
2
3
5
X
arr[5] = arr[4] + arr[3]
6
8
arr[4] = arr[3] + arr[2]
arr[3] = arr[2] + arr[1]
arr[6] = arr[5] + arr[4]
TABULATED FIB(6)
TABULATED VERSION
ALL DONE!
THE REST IS UNDER CONSTRUCTION!
fib(5)
fib(5)
fib(5)
fib(4)
fib(5)
fib(3)
fib(5)
fib(3)
fib(5)
fib(2)
fib(5)
fib(2)
fib(5)
fib(1)
fib(5)
fib(2)
fib(5)
fib(1)
+
+
+
+
0
1
2
3
4
5
1
1
2
3
5
X
RECURSION + MEMOIZATION
What we've already calculated
TOP DOWN VS. BOTTOM UP
An example:
Write a function called stairs which accepts n number of stairs. Imagine that a person is standing at the bottom of the stairs and wants to reach the top and the person can climb either 1 stair or 2 stairs at a time. Your function should return the number of ways the person can reach the top by only climbing 1 or 2 stairs at a time.
Start with something small
Stairs(4)
- 1,1,1,1
- 2,1,1
- 1,2,1
- 1,1,2
- 2,2
Stairs(3)
- 1,1,1
- 1,2
- 2,1
Stairs(2)
- 1,1
- 2
Stairs(1)
- 1
1
2
3
5
8
Stairs(5)
- 1,1,1,1,1
- 2,1,1,1
- 1,2,1,1
- 1,1,2,1
- 2,2,1
- 1,1,1,2
- 1,2,2
- 2,1,2
What are the subproblems?
s(6)
s(5)
s(4)
s(2)
s(3)
s(1)
s(3)
s(3)
s(4)
s(2)
s(2)
s(2)
s(1)
What is the substructure?
stairs(n) = stairs(n - 1) + stairs(n - 2);
This is usually the hardest part of dynamic programming and takes a lot of practice!
How do we solve it?
Brute force
Time Complexity O(2^N)
function stairs(n) {
if (n <= 0) return 0;
if (n <= 2) return n;
return stairs(n - 1) + stairs(n - 2);
}Memoization
Storing the result of an expensive function
Usually done using recursion
Memoization Solution
function stairs(n, memo=[]) {
if (n <= 0) return 0;
if (n <= 2) return n;
if (memo[n] > 0) return memo[n];
memo[n] = stairs(n - 1, memo) + stairs(n - 2, memo);
return memo[n];
}Time Complexity - O(N)
Tabulation
Storing the result of a previous result in a "table" (usually an array)
Usually done using iteration
Better space complexity can be achieved using tabulation
Tabulation Solution
function stairs(n) {
if(n < 3) return n;
let store = [1,1];
for(let i = 2; i <= n; i++) {
let total = store[1] + store[0]
store[0] = store[1]
store[1] = total
}
return store[1];
}Time Complexity - O(N)
Space Complexity - O(1)
Another example
function fib(n) {
if (n <= 0) return 0;
if (n <= 2) return 1;
return fib(n - 1) + fib(n - 2);
}What are the overlapping subproblems?
fib(7)
fib(6)
fib(5)
fib(3)
fib(4)
fib(1)
fib(2)
fib(4)
fib(4)
fib(5)
fib(3)
fib(3)
fib(3)
fib(2)
fib(2)
What is the substructure?
fib(n) = fib(n - 1) + fib(n - 2);
Memoization
function fib(n, savedFib={}) {
// base case
if (n <= 0) { return 0; }
if (n <= 2) { return 1; }
// memoize
if (savedFib[n - 1] === undefined) {
savedFib[n - 1] = fib(n - 1, savedFib);
}
// memoize
if (savedFib[n - 2] === undefined) {
savedFib[n - 2] = fib(n - 2, savedFib);
}
return savedFib[n - 1] + savedFib[n - 2];
}Tabulation
function fib(n){
let arr = [0,1]
// calculating the fibonacci and storing the values
for(let i = 2; i <= n; i++){
arr[i] = arr[i-1] + arr[i-2]
}
return arr[n]
}Using lists and matrices to break down problems
An example:
Write a function called coinChange which accepts two parameters: an array of denominations and a value. The function should return the number of ways you can obtain the value from the given collection of denominations. You can think of this as figuring out the number of ways to make change for a given value from a supply of coins.
Building a list
| 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 |
Amount - 10 / Denominations - [1,2,5]
1
6
2
7
3
8
4
9
5
10
0
If amount > coin:
combinations[amount] += combinations[amount-coin]
Start with 1
Move to 2
| 1 | 1 | 2 | 2 | 3 | 3 | 4 | 4 | 5 | 5 | 6 |
Amount - 10 / Denominations - [1,2,5]
1
6
2
7
3
8
4
9
5
10
0
If amount > coin:
combinations[amount] += combinations[amount-coin]
Current Coin - 2
Move to 5
| 1 | 1 | 2 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 10 |
Amount - 10 / Denominations - [1,2,5]
1
6
2
7
3
8
4
9
5
10
0
If amount > coin:
combinations[amount] += combinations[amount-coin]
Current Coin - 5
Where is this actually used?
- Artificial Intelligence
- Speech Recognition
- Caching
- Image Processing
- Shortest Path Algorithms
- Much, much more!
YOUR
TURN
Greedy Algorithms
A greedy algorithm is an algorithmic paradigm that follows the problem solving heuristic of making the locally optimal choice at each stage with the hope of finding a global optimum.
What?
An algorithm that makes the best guess about what the right answer is and tries to solve it that way as quickly as possible!
Where are they used?
You've seen one already!
Remember how Dijkstra's Algorithm works!
An example:
The coin change problem - again!
A greedy algorithm takes the highest denomination and works it's way down
Pseudocode for Coin Change
- Start with the largest denomination
- Once the total can not use the largest
- Move to the 2nd largest
- Work your way down until there is no more change
Do they work?
Sometimes! Not always!
If we wanted the least amount of coins, a dynamic programming solution would be more efficient
YOUR
TURN
Backtracking
"Backtracking is a general algorithm for finding all (or some) solutions to notably constraint satisfaction problems
It incrementally builds candidates to the solutions, and abandons a candidate ("backtracks") as soon as it determines that the candidate cannot possibly be completed to a valid solution"
What is it?
Going through a solution and retracing steps backward if the solution is not valid.
How does it work?
Where is it used?
Puzzle Solving - Sudoku
N Queens / Rooks
Recap
- Dynamic Programming is the idea of breaking down a problem into smaller subproblems - it's hard
- Optimal substructure is required to use dynamic program and involves figuring out the correct expression to consistently solve subproblems
- Overlapping subproblems is the second essential part of dynamic programming
- Greedy Algorithms are a more aggressive and not always efficient way of solving algorithms
- Backtracking is quite useful when solving for restrictive conditions with unknown possibilities