BINARY HEAPS
OBJECTIVES
Define what a binary heap is
Compare and contrast min and max heaps
Implement basic methods on heaps
Understand where heaps are used in the real world and what other data structures can be constructed from heaps
WHAT IS A BINARY HEAP?
Very similar to a binary search tree, but with some different rules!
In a MaxBinaryHeap, parent nodes are always larger than child nodes. In a MinBinaryHeap, parent nodes are always smaller than child nodes
WHAT DOES IT LOOK LIKE?
41
33
39
12
27
18
NOT A BINARY HEAP
33
41
18
39
27
12
MAX BINARY HEAP
- Each parent has at most two child nodes
- The value of each parent node is always greater than its child nodes
- In a max Binary Heap the parent is greater than the children, but there are no guarantees between sibling nodes.
- A binary heap is as compact as possible. All the children of each node are as full as they can be and left children are filled out first

Value of parent is always greater than children

No Implied Ordering Between Siblings
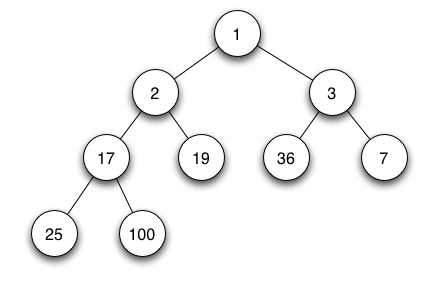
A MIN BINARY HEAP
Why do we need to know this?
Binary Heaps are used to implement Priority Queues, which are very commonly used data structures
They are also used quite a bit, with graph traversal algorithms
We'll come back to this!
REPRESENTING HEAPS
41
33
39
12
27
18
THERE'S AN EASY WAY OF STORING A BINARY HEAP...
A LIST/ARRAY

REPRESENTING A HEAP

REPRESENTING A HEAP
Parent
L Child
R Child
0 1 2 3 4 5 6 7 8 9 10 11 12 13 14

REPRESENTING A HEAP
Parent
L Child
R Child
0 1 2 3 4 5 6 7 8 9 10 11 12 13 14

REPRESENTING A HEAP
Parent
L Child
R Child
0 1 2 3 4 5 6 7 8 9 10 11 12 13 14

REPRESENTING A HEAP
Parent
L Child
R Child
0 1 2 3 4 5 6 7 8 9 10 11 12 13 14

REPRESENTING A HEAP
Parent
L Child
R Child
0 1 2 3 4 5 6 7 8 9 10 11 12 13 14

For any index of an array n...
The left child is stored at 2n + 1
The right child is at 2n + 2
WHAT IF WE HAVE A CHILD NODE AND WANT TO FIND ITS PARENT?

Parent
Child
0 1 2 3 4 5 6 7 8 9 10 11 12 13 14
WHAT IF WE HAVE A CHILD NODE AND WANT TO FIND ITS PARENT?

Parent
Child
0 1 2 3 4 5 6 7 8 9 10 11 12 13 14
For any child node at index n...
Its parent is at index (n-1)/2

floored
DEFINING OUR CLASS
Class Name:
MaxBinaryHeap
Properties:
values = []
Adding to a MaxBinaryHeap
41
33
39
12
27
18
55
- Add to the end
- Bubble up
ADD TO THE END
41
33
39
12
27
18
55
[41,39,33,18,27,12,55]
BUBBLE UP
41
55
39
12
27
18
33
[41,39,33,18,27,12,55]
[41,39,55,18,27,12,33]
BUBBLE UP
55
41
39
12
27
18
33
[41,39,55,18,27,12,33]
[55,39,41,18,27,12,33]
Bubbling Up
55
41
39
12
27
18
33
INSERT PSEUDOCODE
- Push the value into the values property on the heap
- Bubble the value up to its correct spot!
INSERT PSEUDOCODE
- Push the value into the values property on the heap
- Bubble Up:
- Create a variable called index which is the length of the values property - 1
- Create a variable called parentIndex which is the floor of (index-1)/2
- Keep looping as long as the values element at the parentIndex is less than the values element at the child index
- Swap the value of the values element at the parentIndex with the value of the element property at the child index
- Set the index to be the parentIndex, and start over!
YOUR
TURN
REMOVING FROM A HEAP
41
33
39
12
27
18
- Remove the root
- Replace with the most recently added
- Adjust (sink down)
The procedure for deleting the root from the heap (effectively extracting the maximum element in a max-heap or the minimum element in a min-heap) and restoring the properties is called down-heap (also known as bubble-down, percolate-down, sift-down, trickle down, heapify-down, cascade-down, and extract-min/max).
SINK DOWN?
REMOVE AND SWAP
41
33
39
12
27
18
[41,39,33,18,27,12]
REMOVE AND SWAP
12
33
39
41
27
18
[12,39,33,18,27]
REMOVED!
[41,39,33,18,27,12]
SINKING DOWN
12
33
39
27
18
[12,39,33,18,27]
[39,12,33,18,27]
SINKING DOWN
39
33
12
27
18
[39,12,33,18,27]
[39,27,33,18,12]
SINKING DOWN
39
33
27
12
18
[39,27,33,18,12]
REMOVING
- Swap the first value in the values property with the last one
- Pop from the values property, so you can return the value at the end.
- Have the new root "sink down" to the correct spot...
- Your parent index starts at 0 (the root)
- Find the index of the left child: 2 * index + 1 (make sure its not out of bounds)
- Find the index of the right child: 2*index + 2 (make sure its not out of bounds)
- If the left or right child is greater than the element...swap. If both left and right children are larger, swap with the largest child.
- The child index you swapped to now becomes the new parent index.
- Keep looping and swapping until neither child is larger than the element.
- Return the old root!
(also called extractMax)
YOUR
TURN
BUILDING A
PRIORITY QUEUE
WHAT IS A
PRIORITY QUEUE?
A data structure where each element has a priority. Elements with higher priorities are served before elements with lower priorities.
A NAIVE VERSION
priority: 1
priority: 2
priority: 3
priority: 4
priority: 5
Use a list to store all elements
Iterate over the entire thing to find the highest priority element.

NEXT TO
GET HELP



















NEXT TO
GET HELP




Class Name:
PriorityQueue
Properties:
values = []
THE SAME AS BEFORE
Class Name:
Node
Properties:
val
priority
BUT ALSO...
val: "walk dog"
priority: 2
val: "pay bill"
priority: 1
val: "go out"
priority: 3
Val doesn't matter.
Heap is constructed using Priority
- Write a Min Binary Heap - lower number means higher priority.
- Each Node has a val and a priority. Use the priority to build the heap.
- Enqueue method accepts a value and priority, makes a new node, and puts it in the right spot based off of its priority.
- Dequeue method removes root element, returns it, and rearranges heap using priority.
OUR PRIORITY QUEUE
MaxHeapify
Converting an array into a MaxBinaryHeap
- Create a new heap
- Iterate over the array and invoke your insert function
- return the values property on the heap
YOUR
TURN
Heapsort
We can sort an array in O(n log n) time and O(1) space by making it a heap!
- Make the array a max heap (use maxHeapify)
- Loop over the array, swap the root node with last item in the array
- After swapping each item, run maxHeapify again to find the next root node
- Next loop you'll swap the root node with the second-to-last item in the array and run maxHeapify again.
- Once you've run out of items to swap, you have a sorted array!
YOUR
TURN
MinBinaryHeap
12
23
18
44
51
29
Same idea, min values go upwards
Big O of Binary Heaps
Insertion - O(log N)
Removal - O(log N)
Search - O(N)
WHY LOG(N)?

Suppose we wanted to insert 200
200
For 16 Elements....4 comparisons
WHAT ABOUT WORST CASE?
REMEMBER THIS DEPRESSING TREE?
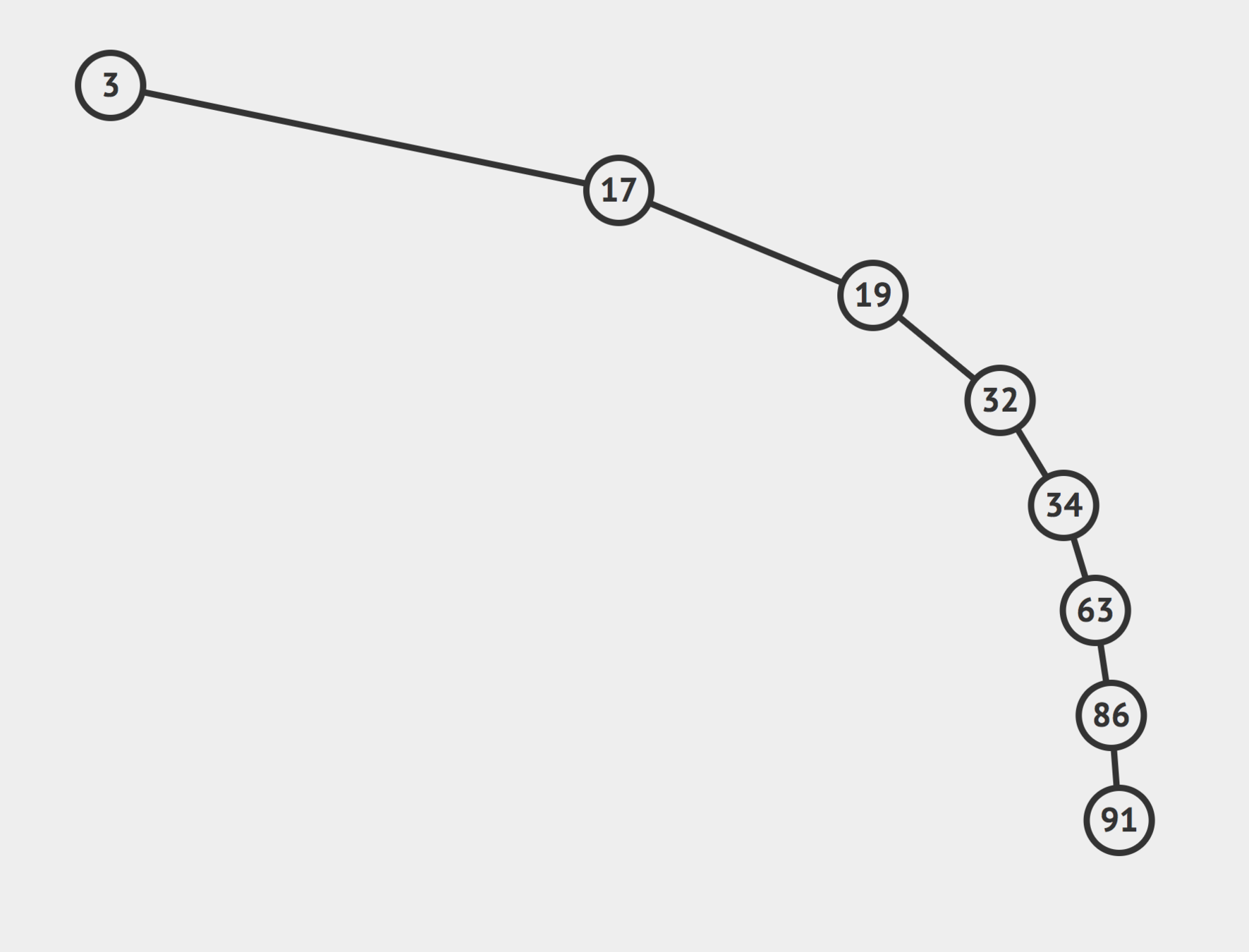
NOT POSSIBLE WITH HEAPS!
RECAP
-
Binary Heaps are very useful data structures for sorting, and implementing other data structures like priority queues
-
Binary Heaps are either MaxBinaryHeaps or MinBinaryHeaps with parents either being smaller or larger than their children
-
With just a little bit of math, we can represent heaps using arrays!
Binary Heaps
By colt_steele
Binary Heaps
- 7,371



