TREES

OBJECTIVES

  • Define what a tree is
  • Compare and contrast trees and lists
  • Explain the differences between trees, binary trees, and binary search trees
  • Implement operations on binary search trees

WHAT IS A TREE?

A data structure that consists of nodes in a parent / child relationship

👩‍👦

TREES

2

12

99

11

2

1

8

9

2

7

44

10

87

55

TREES

2

12

11

9

2

TREES

2

12

12

11

2

1

8

9

2

7

44

Lists - linear

Trees - nonlinear

A Singly Linked List

(sort of a special case of a tree)

2

12

11

2

12

11

NOT A TREE

2

12

11

8

9

2

44

NOT A TREE

2

12

11

8

9

2

44

TREE TERMINOLOGY

  • Root - The top node in a tree.
  • Child -A node directly connected to another node when moving away from the Root.
  • Parent - The converse notion of a child.
  • Siblings -A group of nodes with the same parent.
  • Leaf - A node with no children.
  • Edge - The connection between one node and another.

KINDS OF TREES

  • Trees
  • Binary Trees
  • Binary Search Trees

2

12

12

11

2

1

8

9

2

7

44

TREES

Lots of different applications!

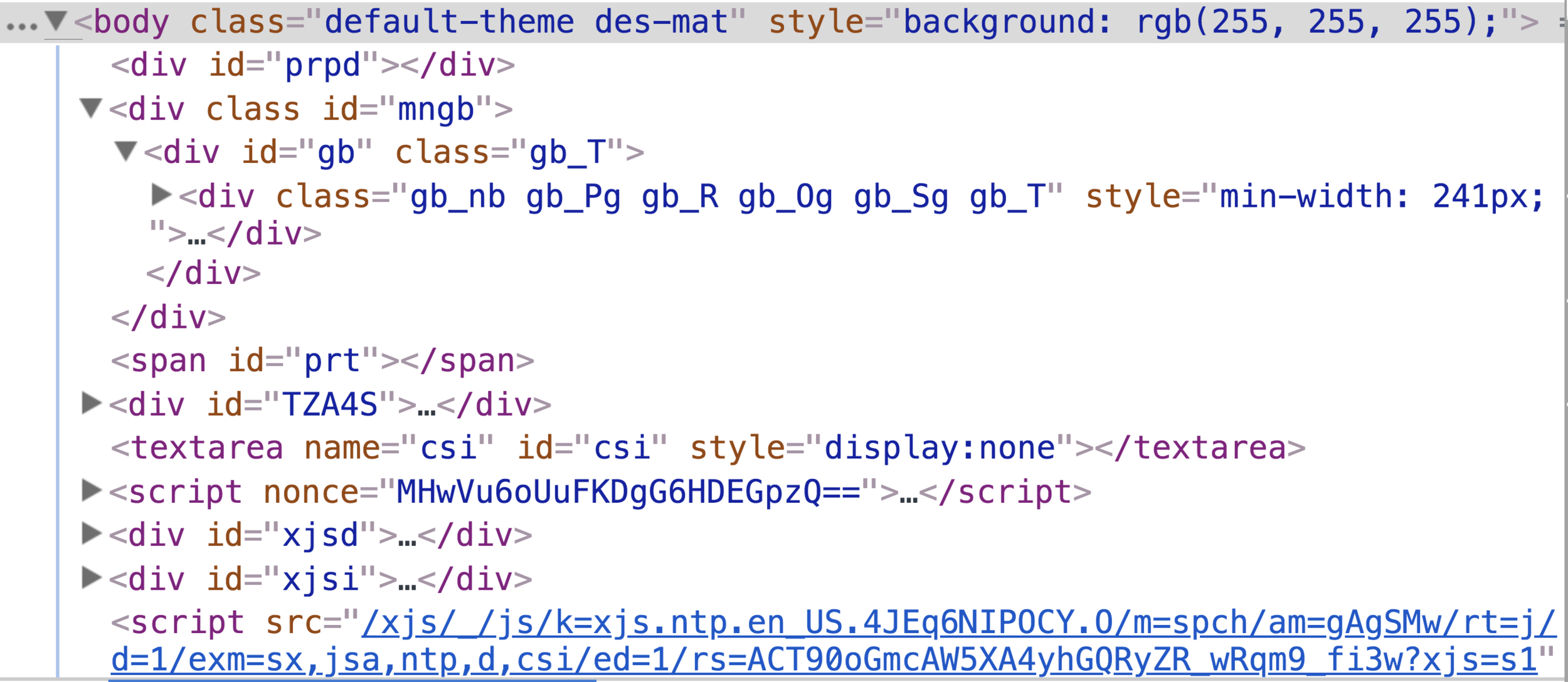
  • HTML DOM
  • Network Routing
  • Abstract Syntax Tree
  • Artificial Intelligence
  • Folders in Operating Systems
  • Computer File Systems

TREES

BINARY TREES

1

5

12

11

3

6

NOT A BINARY TREE

1

5

12

11

3

6

9

Lots of different applications as well!

  • Decision Trees (true / false)
  • Database Indicies
  • Sorting Algorithms

BINARY TREES

BINARY SEARCH TREES

10

6

15

20

8

3

HOW BSTS WORK

  • Every parent node has at most two children
  • Every node to the left of a parent node is always less than the parent
  • Every node to the right of a parent node is always greater than the parent

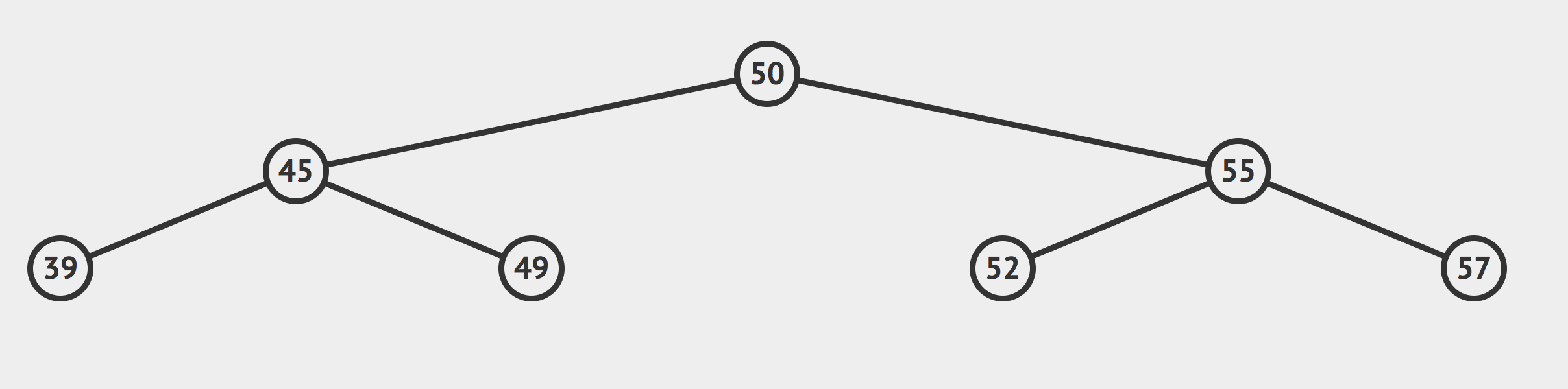
Is this a valid BST?

10

8

15

20

6

3

NOPE

Is this a valid BST?

10

8

15

20

6

3

NOPE!

4

Is this a valid BST?

10

8

15

20

6

3

NOPE!

4

The BinarySearchTree Class 

class BinarySearchTree {
    constructor(){
        this.root = null;
    }
}
class Node {
    constructor(value){
        this.value = value;
        this.left = null;
        this.right = null;
    }
}

INSERTING

10

6

15

20

8

3

13

10

6

15

20

8

3

13

INSERTING

INSERTING A NODE

Steps - Iteratively or Recursively

  • Create a new node
  • Starting at the root
    • Check if there is a root, if not - the root now becomes that new node!
    • If there is a root, check if the value of the new node is greater than or less than the value of the root
    • If it is greater 
      • Check to see if there is a node to the right
        • If there is, move to that node and repeat these steps
        • If there is not, add that node as the right property
    • If it is less
      • Check to see if there is a node to the left
        • If there is, move to that node and repeat these steps
        • If there is not, add that node as the left property

YOUR

TURN

Finding a Node in a BST

Steps - Iteratively or Recursively

  • Starting at the root
    • Check if there is a root, if not - we're done searching!
    • If there is a root, check if the value of the new node is the value we are looking for. If we found it, we're done!
    • If not, check to see if the value is greater than or less than the value of the root
    • If it is greater 
      • Check to see if there is a node to the right
        • If there is, move to that node and repeat these steps
        • If there is not, we're done searching!
    • If it is less
      • Check to see if there is a node to the left
        • If there is, move to that node and repeat these steps
        • If there is not, we're done searching!

Let's visualize this!

YOUR

TURN

Big O of BST

Insertion - O(log n)

Searching - O(log n)

NOT guaranteed!

Double the number of nodes...

You only increase the number of steps to insert/find by 1

2x number of nodes: 1 extra step

4x number of nodes: 2 extra steps

8x number of nodes: 3 extra steps

Big O of BST

Insertion - O(log n)

Searching - O(log n)

NOT guaranteed!

NOT guaranteed!

😬

😬

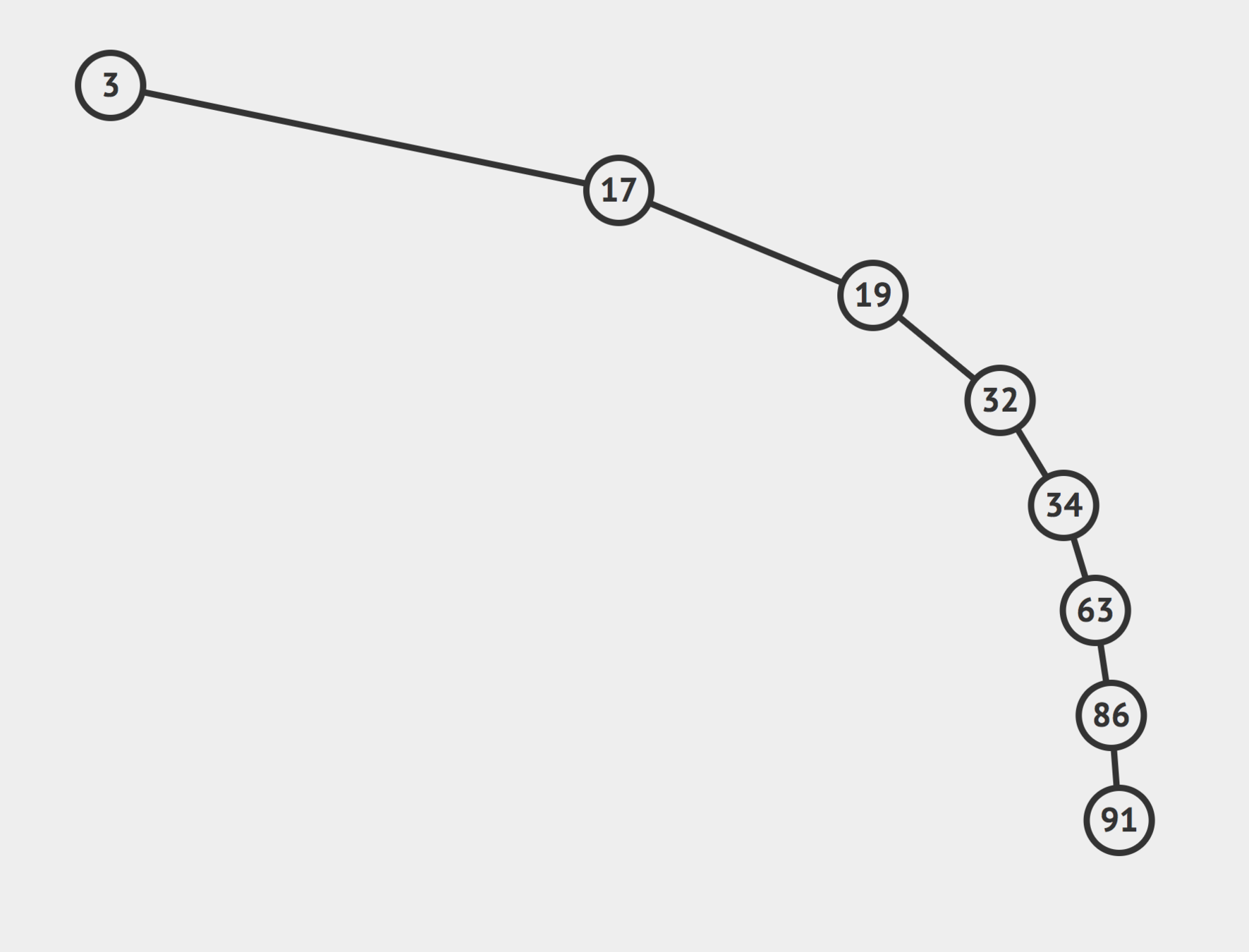
THIS IS A VALID BINARY SEARCH TREE

TREE

TRAVERSAL

VISIT EVERY NODE ONCE

10

19

6

20

8

99

TRAVERSING A TREE

Two ways:

  • Breadth-first Search
  • Depth-first Search

BREADTH

 FIRST SEARCH

BFS

10

6

15

20

8

3

[10, 6, 15, 3, 8, 20]

Steps - Iteratively

  • Create a queue (this can be an array) and a variable to store the values of nodes visited
  • Place the root node in the queue
  • Loop as long as there is anything in the queue
    • Dequeue a node from the queue and push the value of the node into the variable that stores the nodes
    • If there is a left property on the node dequeued - add it to the queue
    • If there is a right property on the node dequeued - add it to the queue
  • Return the variable that stores the values

BFS

YOUR

TURN

DEPTH FIRST SEARCH

DFS - InOrder

10

6

15

20

8

3

Let's visualize this!

[3, 6, 8, 10, 15, 20]

DFS - InOrder

10

6

15

20

8

3

Let's visualize this!

[3, 6, 8, 10, 15, 20]

Steps - Recursively

DFS - InOrder

  • Create a variable to store the values of nodes visited
  • Store the root of the BST in a variable called current
  • Write a helper function which accepts a node
    • If the node has a left property, call the helper function with the left property on the node
    • Push the value of the node to the variable that stores the values
    • If the node has a right property, call the helper function with the right property on the node
  • Invoke the helper function with the current variable
  • Return the array of values

DFS - PreOrder

10

6

15

20

8

3

Let's visualize this!

[10, 6, 3, 8, 15, 20]

Steps - Recursively

DFS - PreOrder

  • Create a variable to store the values of nodes visited
  • Store the root of the BST in a variable called current
  • Write a helper function which accepts a node
    • Push the value of the node to the variable that stores the values
    • If the node has a left property, call the helper function with the left property on the node
    • If the node has a right property, call the helper function with the right property on the node
  • Invoke the helper function with the current variable
  • Return the array of values

DFS - PostOrder

10

6

15

20

8

3

Let's visualize this!

[3, 8, 6, 20, 15, 10]

Steps - Recursively

DFS - PostOrder

  • Create a variable to store the values of nodes visited
  • Store the root of the BST in a variable called current
  • Write a helper function which accepts a node
    • If the node has a left property, call the helper function with the left property on the node
    • If the node has a right property, call the helper function with the right property on the node
    • Push the value of the node to the variable that stores the values
    • Invoke the helper function with the current variable
  • Return the array of values

YOUR

TURN

BFS?

DFS?

Which is better?

BREADTH FIRST

Lots of nodes to keep track of!

DEPTH FIRST

Fewer nodes to keep track of

BREADTH FIRST

Fewer nodes to keep track of

DFS - InOrder

10

6

15

20

8

3

[3, 6, 8, 10, 15, 20]

Used commonly with BST's

Notice we get all nodes in the tree in their underlying order

DFS - PreOrder

10

6

15

20

8

3

[10, 6, 3, 8, 15, 20]

Can be used to "export" a tree structure so that it is easily reconstructed or copied.

RECAP

  • Trees are non-linear data structures that contain a root and child nodes
  • Binary Trees can have values of any type, but at most two children for each parent
  • Binary Search Trees are a more specific version of binary trees where every node to the left of a parent is less than it's value and every node to the right is greater
  • We can search through Trees using BFS and DFS

Removing a Node in a BST

This one can be tough!

No Children, No Problem

Let's visualize this!

10

6

18

20

8

3

15

Steps - Iteratively

  • Find the parent of the node that needs to be removed and the node that needs to be removed
  • If the value we are removing is greater than the parent node
    • Set the right property of the parent to be null
  • If the value we are removing is less than the parent node​
    • Set the left property of the parent to be null
  • Otherwise, the node we are removing has to be the root, so set the root to be null

Removing a Node - 0 children

One Child, One Problem

Let's visualize this!

10

6

18

20

8

3

One Child, One Problem

Let's visualize this!

10

6

8

3

20

Steps - Iteratively

Removing a Node - 1 child

  • Find the parent of the node that needs to be removed and the node that needs to be removed
  • See if the child of the node to be removed is on the right side or the left side
  • If the value we are removing is greater than the parent node​​
    • Set the right property of the parent to be the child
  • If the value we are removing is less than the parent node​
    • Set the left property of the parent to be the child
  • Otherwise, set the root property of the tree to be the child

Two Children, More Problems

Let's visualize this!

10

6

18

20

8

3

15

Find the Predecessor Node!

10

6

18

20

8

3

15

6

18

20

8

3

15

One Right, As left as possible

Steps - Iteratively

  • Find the parent of the node that needs to be removed and the node that needs to be removed
  • Find the predecessor node and store that in a variable
  • Set the left property of the predecessor node to be the left property of the node that is being removed
  • If the value we are removing is greater than the parent node​​
    • Set the right property of the parent to be the right property of the node to be removed
  • If the value we are removing is less than the parent node​
    • Set the left property of the parent to be the right property of the node to be removed
  • Otherwise, set the root of the tree to be the right property of the node to be removed

Removing a Node - 2 children

YOUR

TURN